本期,边肖将为您带来关于python如何绘制酷动态Julia集的信息。文章内容丰富,从专业角度进行分析和描述。希望你看完这篇文章能有所收获。
00-1010这个Julia不是Julia,指的是使迭代公式F (z)=Z 2C F (z)=Z 2C F (z)=Z 2C C收敛于某个复数c c c的复数z z的集合例如,当c=0 c=0 c=0时,其收敛区间为z 2 nbsp。
; < 1 z^2<1 z2<1的单位圆,对应的 c c c的Julia集便是 cos θ + i sin θ \cos\theta+i\sin\theta cosθ+isinθ。
Mandelbrot集
特别地,当 c = z c=z c=z的初始值时,符合收敛条件的 z z z的便构成大名鼎鼎的Mandelbrot集
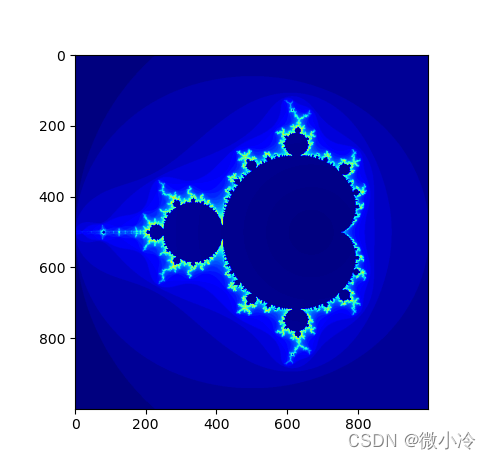
在上图中,颜色表示该点的发散速度,可以理解为开始发散时迭代的次数。其生成代码也非常简单,唯一需要注意的是,由于使用了大量的矩阵运算,故使用了cupy,如果电脑没装cuda,只需将所有的cp改为np即可。
# 这些代码会在后面的程序中反复调用,不再说明
import numpy as np
import time
import matplotlib.pyplot as plt
import cupy as cp
#生成z坐标 x0,y0 为起始点, nx,ny为点数, delta为点距
def genZ(x0, y0, nx, ny, delta):
real, img = cp.indices([nx,ny])*delta
real += x0
img += y0
return real.T+img.T*1j
#获取Julia集,n为迭代次数,m为判定发散点,大于1即可
def getJulia(z,c,n,m=2):
t = time.time()
z,out = z*1, cp.abs(z)
c = cp.zeros_like(z)+c
for i in range(n):
absz = cp.abs(z)
z[absz>m]=0 #对开始发散的点置零
c[absz>m]=0
out[absz>m]=i #记录发散点的发散速度
z = z*z + c
print("time:",time.time()-t)
return out
z1 = genZ(-2,-1.5,1000,1000,0.003)
mBrot = getJulia(z1,z1,50)
plt.imshow(mBrot.get(), cmap=plt.cm.jet)
plt.show()
如果对其生成过程感兴趣,那么可以观察一下随着迭代次数的增加,图像的变化情况

代码如下。
from matplotlib import animation
fig = plt.figure()
fig.subplots_adjust(top=1, bottom=0, left=0, right=1)
ax = plt.subplot()
def getJulias(z,c,n,m=2):
z,out = z*1, cp.abs(z)
c = cp.zeros_like(z)+c
J = []
for i in range(n):
z = z*z + c
absz = cp.abs(z)
z[absz>m]=0 #对开始发散的点置零
c[absz>m]=0
out[absz>m]=i #记录发散点的发散速度
im = ax.imshow(out.get(),cmap=plt.cm.jet, animated=True)
ax.set_axis_off()
J.append([im])
return J
N = 75 #迭代次数
z1 = genZ(-2,-1.5,1000,1000,0.003)
J = getJulias(z1,z1,N)
ani = animation.ArtistAnimation(fig, J, interval=50, blit=True,repeat_delay=1000)
plt.show()
ani.save('julias.gif',writer='imagemagick')
无限缩放
Mandelbrot集的分形特征意味着我们所生成的图片可以无限放大,但是受到栅格化尺寸的影响,手动的放大并不会更改其真实尺寸,
为了照顾观感,将缩放中心作为图像的中心,所以对genZ函数进行修改。如果选取(-0.75,-0.2)作为缩放中心,则其变化如下

代码为
from matplotlib import animation
# 生成z坐标 xy=np.array([xc,yc]) 为起始点,
# nxy=np.array([nx,ny])为点数, delta为点距
def genZbyCenter(xy,nxy,delta):
x0, y0 = xy-np.array(nxy)*delta/2
return genZ(x0,y0,*nxy,delta)
mBrots = []
xy = [-0.75,-0.2]
nxy = [1000,1000]
delta0 = 0.003 #初始宽度
fig = plt.figure()
fig.subplots_adjust(top=1, bottom=0, left=0, right=1)
ax = plt.subplot()
for n in range(50):
z1 = genZbyCenter(xy,nxy,1.1**(-n)*delta0)
out = getJulia(z1,z1,40)
im = ax.imshow(out.get(),cmap=plt.cm.jet, animated=True)
ax.set_axis_off()
mBrots.append([im])
ani = animation.ArtistAnimation(fig, mBrots, interval=50, blit=True)
plt.show()
ani.save('zoom.gif',writer='imagemagick')
Julia集
如果更改c的值,那么就能得到一个变化着的Julia集,例如,下面选取一条直线
y = x y=x y=x
上面的Julia集,效果如图所示

代码为
z1 = genZ(-2,-1.5,1000,1000,0.003)
fig = plt.figure()
fig.subplots_adjust(top=1, bottom=0, left=0, right=1)
ax = plt.subplot()
mBrots = []
for x in np.arange(0.5,1,0.01):
c = x + x*1j
out = getJulia(z1,c,40)
im = ax.imshow(out.get(),cmap=plt.cm.jet, animated=True)
ax.set_axis_off()
mBrots.append([im])
ani = animation.ArtistAnimation(fig, mBrots, interval=50)
plt.show()
ani.save('julia.gif',writer='imagemagick')
上述就是小编为大家分享的python如何绘制超炫酷动态Julia集了,如果刚好有类似的疑惑,不妨参照上述分析进行理解。如果想知道更多相关知识,欢迎关注行业资讯频道。
内容来源网络,如有侵权,联系删除,本文地址:https://www.230890.com/zhan/144748.html
