本文主要讲解“Python如何计算点到直线的距离和直线之间的交角”。本文的解释简单明了,易学易懂。请跟随边肖的思路学习学习“Python如何计算点到直线的距离和直线之间的交角”!
前言
项目中,会有计算点到直线距离、两条直线交点坐标、两条直线夹角的要求。
一、点到直线距离计算
因为在项目中最容易得到点的坐标,所以最清楚的是用矢量法进行所有的数学计算。用矢量法推导出点到直线的距离。
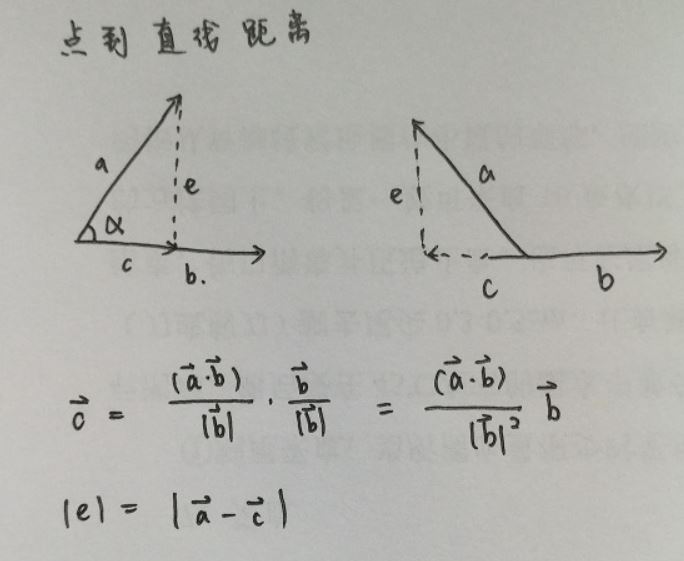
importnumpayasnp
array_longi=np.array([x2-x1,y2-y1])
array _ trans=NP . array([x2-line _ start _ x,y2-line_start_y])
#矢量点对点计算示例
array _ temp=(float(array _ trans . dot(array _ longi))/array _ longi . dot(array _ longi))
array_temp=array_longi .点(array_temp)
distance=NP . sqrt((array _ trans-array _ temp)。点(数组_ trans-array _ temp)) #距离
二、两条直线交点坐标计算
一般方程法:
直线的一般方程是F(x)=ax乘以c=0。假设直线的两点是(x0,y0)和(x1,y1),那么a=y0y1,b=x1x0,c=x0 y1x1y 0就可以得到。
因此,两条直线可以表示为
F0(x)=a0*x b0*y c0=0
F1(x)=a1*x b1*y c1=0
那么两条直线的交点应该满足
a0*x b0*y c0=a1*x b1*y c1
由此可以推断。
x=(B0 * C1B1 * c0)/D
y=(a1 * c0A0 * C1)/D
D=A0 * B1A1 * B0,(当D为0时,两条直线平行)
事实上,它们是联立方程的叉积应用。
F0(x)=a0*x b0*y c0=0
F1(x)=a1*x b1*y c1=0
i j k
a0 b0 c0
a1 b1 c1
分类点:
x=0
y=0
def__init__(self,x=0,y=0):
self.x=x
self.y=y
类别:
def__init__(self,p1,p2):
self.p1=p1
self.p2=p2
defGetLinePara(线路):
line.a=line.p1.y-line.p2.y
line.b=line.p2.x-line.p1.x
line . c=line . P1 . x * line . p2 . y-ine . p2 . x * line . P1 . y
定义交叉点(l1,l2):
GetLinePara(l1)
GetLinePara(l2)
d=l1.a*l2.c-l2.a*l1.b
p=点()
p . x=(L1 . b * L2 . c-L2 . b * L1 . c)* 1.0/d
p . y=(L1 . c * L2 . a-L2 . c * L1 . a)* 1.0/d
p1=点(1,1)
p2=点(3,3)
线1=线(p1,p2)
p3=点(2,3.1)
p=点(3.1,2)
line2=Line(p3,p4)
PC=Get交叉点(第1行,第2行)
Print(Pc.x,Pc.y)
三、两条直线夹角计算
用矢量法求两条直线的夹角。这个思路类似于求点到直线的距离,也是用余弦定理。

importnumpayasnp
defGetCrossAngle(l1,l2):
arr _ 0=NP . array([(L1 . p2 . x-L1 . P1 . x),(l1.p2.y-l1.p1.y)]
arr _ 1=NP . array([(L2 . p2 . x-L2 . P1 . x),(l2.p2.y-l2.p1.y)]
cos _ value=(float(arr _ 0 . dot(arr _ 1))/(NP . sqrt(arr _ 0 . dot(arr _ 0))* NP . sqrt(arr _ 1 . dot(arr _ 1)))
returnnp . arccos(cos _ value)*(180/NP . pi)
Angle=getcrossangle(第1行,第2行)#感谢阅读。以上就是“Python如何计算点到直线的距离以及直线之间的交角”的内容。看完这篇文章,相信大家对Python如何计算点到直线的距离以及直线之间的交角有了更深的理解,具体用法还需要实践验证。在这里,边肖将为您推送更多关于知识点的文章,敬请关注!
内容来源网络,如有侵权,联系删除,本文地址:https://www.230890.com/zhan/155607.html
