pagerank算法原理举例子(pagerank算法详解)

我相信很多没有经验的人对PageRank算法如何对网页进行排名一窍不通。为此，本文总结了问题产生的原因及解决方法。希望你能通过这篇文章解决这个问题。

1，PageRank 算法原理

PageRank算法的核心原理是：在互联网中，如果一个网页被很多其它网页所链接，说明该网页非常的重要，那么它的排名就高.

拉里佩奇把整个互联网看成一个大图，每个网站就像一个节点，每个网页的链接就像一条弧线。然后，互联网可以用图或矩阵来描述。

拉里佩奇也因为这个算法在30岁的时候被选为美国工程院院士。

假设目前有四个网页，即A，B，C，D,它们的链接如下：

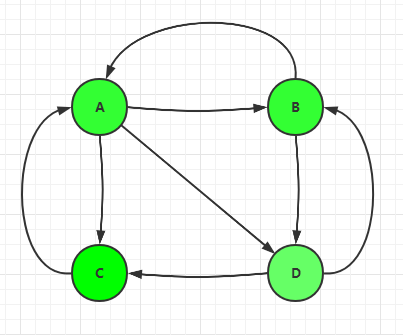
我们规定有两种链条：

链外：从自身拉出的链条。

进入链条：从外部引入自身的链条。

例如，图中的C网页有两个传入链接和一个传出链接。

PageRank的想法是，一个网页的影响力就等于它的所有入链的影响力之和.

用数学公式表示如下：

其中(分数代表页面影响力):

PR(u)是网页u的分数。

Bu是网页u的链式集合。

网页V是网页u的任意链接

PR(v)是净v的分数。

L(v)是链外的网页数v。

网页V给网页U带来的评分是PR(v)/L(v)。

那么PR(u)等于所有链入口分数之和。

在上面的公式中，我们假设从一个页面v 到达它的所有的出链页面的概率是相等的.

例如，在上图中，A页面有三个指向B、C、D.的出站链接。然后，当用户访问A,时，有可能跳转到B、C或D,跳转概率是1/3.

00-1010我们来看看如何计算网页的分数。

我们可以用一个表格来显示上图中网页的链接关系，以及每个页面到其他页面的概率：

ABCDA0 A-A1/2 B- A1 C-A0 D-AB1/3 A-B0 B- B0 C-B1/2D-BC1/3 A-C0 B- C0 C-C1/2D-CD1/3 A-D

d>1/2 B->D0 C->D0 D->D

根据这个表格中的数字，可以将其转换成一个矩阵M：

假设 A、B、C、D 四个页面的初始影响力都是相同的，都为 1/4，即：

经过第一次分值转移之后，可以得到 W₁，如下：

同理可以得到W₂，W₃ 一直到 W_n：

• W₂ = M * W₁

• W₃ = M * W₂

• W_n = M * W_n-1

那么什么时候计算终止呢？

佩奇和布林已经证明，不管网页的初识值选择多少（我们这假设都是1/4），最终都能保证网页的分值能够收敛到一个真实确定值。

也就是直到 W_n 不再变化为止。

这就是网页分值的计算过程，还是比较好理解的。

3，PageRank 的两个问题

我们上文中介绍到的是PageRank 的基本原理，是简化版本。在实际应用中会出现等级泄露（RankLeak）和等级沉没（Rank Sink）的问题。

如果一个网页没有出链，就会吸收其它网页的分值不释放，最终会导致其它网页的分值为0，这种现象叫做等级泄露。如下图中的网页C：

相反，如果一个网页没有入链，最终会导致该网页的分值为0，这种现象叫做等级沉没。如下图中的网页C：

4，PageRank 的随机浏览模型

为了解决上面的问题，拉里·佩奇提出了随机浏览模型，即用户并不都是依靠网页链接来访问网页，也有可能用其它方式访问网址，比如输入网址。

因此，提出了阻尼因子的概念，这个因子代表用户按照跳转链接来上网的概率，而 1-d 则代表用户通过其它方式访问网页的概率。

所以，将上文中的公式改进为：

其中：

• d 为阻尼因子，通常可以取0.85。

• N 为网页总数。

5，用代码计算网页分值

如何用代码来计算网页的PR 分值呢？（为了方便查看，我把上图放在这里）

我们可以看到，该图实际上就是数据结构中的有向图，因此我们可以通过构建有向图来构建 PageRank 算法。

NetworkX 是一个Python 工具包，其中集成了常用的图结构和网络分析算法。

我们可以用 NetworkX 来构建上图中的网络结构。

首先引入模块：

import networkx as nx

用 DiGraph 类创建有向图：

G = nx.DiGraph()

将4 个网页的链接关系，用数组表示：

edges = [
  ("A", "B"), ("A", "C"), ("A", "D"), 
  ("B", "A"), ("B", "D"), 
  ("C", "A"), 
  ("D", "B"), ("D", "C")
  ]

数组中的元素作为有向图的边，并添加到图中：

for edge in edges:    
    G.add_edge(edge[0], edge[1])

使用pagerank 方法计算PR 分值：

# alpha 为阻尼因子
PRs = nx.pagerank(G, alpha=1)
print PRs

输出每个网页的PR 值：

{'A': 0.33333396911621094, 
 'B': 0.22222201029459634, 
 'C': 0.22222201029459634, 
 'D': 0.22222201029459634}

最终，我们计算出了每个网页的PR 值。

6，画出网络图

NetworkX 包中还提供了画出网络图的方法：

import matplotlib.pyplot as plt

# 画网络图
nx.draw_networkx(G)
plt.show()

如下：

我们还可以设置图的形状，节点的大小，边的长度等属性。

PageRank 算法给了我们一个很重要的启发，权重在很多时候是一个非常重要的指标。

• 比如在人际交往中，个人的影响力不仅取决于你的朋友的数量，而且朋友的质量非常重要，说明了圈子的重要性。

• 比如在自媒体时代，粉丝数并不能真正的代表你的影响力，粉丝的质量也很重要。如果你的粉丝中有很多大V，那么将大大增加你影响力。

看完上述内容，你们掌握PageRank算法如何给网页排名的方法了吗？如果还想学到更多技能或想了解更多相关内容，欢迎关注行业资讯频道，感谢各位的阅读！