python光学仿真如何实现光线追迹折射与反射

本文是关于python光学模拟如何实现光线跟踪折射和反射。边肖觉得很实用，所以想分享给大家学习。希望大家看完这篇文章能有所收获。话不多说，让我们和边肖一起看看。

00-1010光与光学元件相互作用，但只有两种东西，反射和透射。目前光学元件只有平面和球面两种，二维后简化为光线与线段、光线与下弧的关系。

00-1010无论从哪个角度看，平面的反射和折射都比球面简单，反射问题也比折射简单，所以我们先来处理平面的反射问题。

反射定律意味着入射角等于反射角。考虑到这一点，最常规的思维方式一定是求入射光与平面的夹角，然后利用这个夹角和平面在空间中的斜率(在二维空间中是直线)由这个斜率和入射角得到出射光的斜率，进而得到出射光的方程。

这种方法的问题是三角函数和反三角函数需要反复使用，三角函数和反三角函数并不是严格对立的，因此在传递参数的过程中可能会遇到一些麻烦。

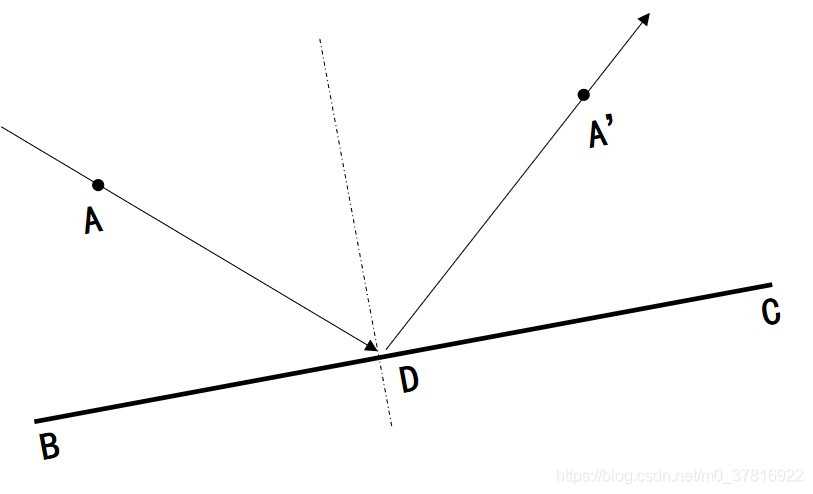
相对来说，比较不容易出错的方法是找到入射点相对于法线的对称点，然后对称点和交点之间的联系就是出射光的方程。

00-1010折射和反射的想法是一样的。最初的想法仍然是先得到入射角，然后根据折射定律计算入射角，再根据出射角求出出射光的表达式。这个思路的难点还是在于三角函数和反函数之间的转换。

至此，我们发现折射和反射在表现形式上是相通的。如果入射点垂直于法线，垂足为c，这个垂线与出射光的交点约定为出射点b，那么出射点到垂足的距离BC与入射点到垂足的距离AC成正比。当入射光线和反射光线的折射率相等时，比值为1，否则比值为\。

我们还可以发现，这个\不一定有解，因为分母中有根表达式，当内部值小于0时，自然没有解。这与我们的物理直觉是一致的，即不是所有的入射光线都有折射光线，当折射光线消失时，就会发生全反射。

因此，根据入射点找到垂足并轻松获取是势在必行的。

然后，对于我们熟悉的折射问题，可以先使入射点关于反射面对称一次，再使其关于定比延长线对称一次，就可以得到出射点。

00-1010到目前为止，我们已经完全建立了一套反射和折射的关系，代码如下：

#得到该点关于直线的对称点，k为比例系数。

defgetSymDot(点，线，k=1):

returntuple((np.array(getPedal(点，线))*(1k)-点)/k)

#获取直线的垂直脚。

定义踏板(点、线):

a，b，c=线

x0，y0=点

y1=(a * * 2 * y0-a * b * x0-b * c)/(a * * 2 b * * 2)

x1=(b * * 2 * x0-a * b * y0-a * c)/(a * * 2 b * * 2)

return(x1，y1)函数getSymDot通过输入点和线来求解对称点，其思想是将点关于线的对称问题转化为点关于垂足的对称问题。因此，引用了GetBudget函数。

这个函数通过输入一点和线来返回过点做线的垂线所得到的垂足。

所有代码都是对上述数学公式的简单复现。

def cataDioLine(abc=[1,-1,1],line=[2,-1,1],
                sPoint=[],cross=[],n1=1,n2=1.5):
    normal = [-line[1],line[0],line[1]*cross[0]-line[0]*cross[1]]#法线
    flecDot = getSymDot(sPoint,normal)
    flec=getABC([cross,flecDot])
    dPara = np.sqrt(line[0]**2+line[1]**2)
    dNormal = np.abs(np.array(normal).dot(list(sPoint)+[1]))/dPara#到法线距离
    dPane = np.abs(np.array(line).dot(list(sPoint)+[1]))/dPara#到反射面距离
    if dNormal == 0:
        return flec,abc
    delt = (n2/n1)**2*(1+(dPane/dNormal)**2)-1#判定全反射
    if delt>0:
        k =dPane/dNormal/np.sqrt(delt)
        fracDot = getSymDot(sPoint,normal,k)
        fracDot = getSymDot(fracDot,line)
        frac = getABC([cross,fracDot])
        return flec,frac
    return flec,[0,0,0]

函数cataDioLine则是反射折射的实现函数。注意，在此引入的getABC并不是此前定义的通过点和角度求表达式的函数，而是通过两点转[a,b,c]的函数。

那么我们是否可以写一个同名函数来实现不同的功能呢？很遗憾的是，Python不支持函数的重载，所以只能将同名函数封装在一起：

def getABC(*par):
    if len(par)==1:     #此时传入的参数为点对dots=[(x0,y0),(x1,y1)]
        dots = par[0]
        abc = [dots[1][1]-dots[0][1],
                dots[0][0]-dots[1][0], 
                -np.linalg.det(dots)]
        return np.array(abc)/(np.sqrt(abc[0]**2+abc[1]**2))
    elif len(par)==2:   #此时传入的参数为点和角度(x0,y0),theta
        theta,sPoint = par
        a,b = [np.sin(theta),-np.cos(theta)]
        c = -(a*sPoint[0]+b*sPoint[1])
        return [a,b,c]

看到输入参数(*par)，我们很多人可能会产生某些不是很美妙的联想，但不要兴奋，这只是python的一种传参方式。(*args)表示将传入的参数组成一个列表args；(**kargs)表示将传入的参数组成一个字典kargs。

弧面问题

光线在弧面上的反射问题，是典型的那种看似复杂实则简单的纸老虎问题，简单到我们只要找到法线就能轻松地转化为平面问题。

所以，问题被简单地转化为求解圆的切线问题——这个切线即反射平面。由于数学过程过于简单，就不写公式了，读者可以试着看代码反推公式。

#获取过交点的圆弧的切线
def getTangent(corss=[0,1],circle=[0,0,1]):
    a = corss[0]-circle[0]
    b = corss[1]-circle[1]
    c = -a*corss[0]-b*corss[1]
    return [a,b,c]

至此，我们就可以得到一个完整的折射反射问题的求解方案：

#光在直线或弧线表面的反折射
def cataDio(abc=[1,-1,1],dots=[(0,2),(2,2)],
            sPoint=[-2,-1],n1=1,n2=1.5):
    cross = getCross(abc,dots,sPoint)           #获取交点
    if cross == []:
        return [],[],[]
    if len(dots)==3:
        line = getTangent(cross,arc2cir(dots))  #圆上切线
    elif len(dots)==2:
        line = getABC(dots)
    flec,frac = cataDioLine(abc,line,sPoint,cross,n1,n2)
    return cross,flec,frac

当然，这里的getCross也需要重新写成不仅适合直线，而且适合弧线的形式：

def getCross(abc=[1,-1,0],dots=[[0,-1],[0,1],[0.5,0]],point=[]):
    if len(dots)==3:
        return getCrossArc(abc,dots,point)
    if len(dots)==2:
        return getCrossDots(abc,dots,point)

这时我们发现用两个点表示线段，三个点表示弧线还是比较舒服的一种做法，至少二者在表达形式上的统一似乎能为我们带来某种内心的愉悦。

以上就是python光学仿真如何实现光线追迹折射与反射，小编相信有部分知识点可能是我们日常工作会见到或用到的。希望你能通过这篇文章学到更多知识。更多详情敬请关注行业资讯频道。